Why You Should (or Shouldn't) be Using Google's JAX in 2023

Since Google's JAX hit the scene in late 2018, it has been steadily growing in popularity, and for good reason. DeepMind announced in 2020 that it is using JAX to accelerate its research, and a growing number of publications and projects from Google Brain and others are using JAX. With all of this buzz, it seems like JAX is the next big Deep Learning framework, right?

Wrong. In this article we’ll clarify what JAX is (and isn’t), why you should care (or shouldn't, but you probably should), and whether you should (or shouldn’t) use it.

Let’s dive in!

What is Google's JAX?

It may be best to start off with what JAX is not. JAX is not a Deep Learning framework or library, and it is not designed to ever be a Deep Learning framework or library in and of itself. In a sentence, JAX is a high performance, numerical computing library which incorporates composable function transformations^[1]. As we can see, Deep Learning is just a small subset of what JAX can do:

Why Should I Care About JAX?

In short - speed. This is the universal aspect of JAX that is relevant for any use case.

Let's sum the first three powers of a matrix (element-wise) with both NumPy and JAX. First up is our NumPy implementation:

def fn(x):
  return x + x*x + x*x*x

x = np.random.randn(10000, 10000).astype(dtype='float32')
%timeit -n5 fn(x)

5 loops, best of 5: 478 ms per loop

We find that this calculation takes about 478 ms. Next, we implement this calculation with JAX:

jax_fn = jit(fn)
x = jnp.array(x)
%timeit jax_fn(x).block_until_ready()

100 loops, best of 5: 5.54 ms per loop

JAX performs this calculation in only 5.54 ms - over 86 times faster than NumPy.

... that's 8,600%.

Perspectives

Things are not quite as simple as "use JAX and your programs will be 86 times faster", but there are still a ton of reasons to use JAX. Since JAX provides a general foundation for high performance scientific computing, it will be useful to different people in different fields for different reasons. Fundamentally, if you are in any field relating to scientific computing, you should care about JAX.

Here are some reasons why you might want to use JAX:

1. NumPy on Accelerators - NumPy is one of the fundamental packages for scientific computing with Python, but it is compatible only with CPU. JAX provides an implementation of NumPy (with a near-identical API) that works on both GPU and TPU extremely easily. For many users, this alone is sufficient to justify the use of JAX.

2. XLA - XLA, or Accelerated Linear Algebra, is a whole-program optimizing compiler, designed specifically for linear algebra. JAX is built on XLA, raising the computational-speed ceiling significantly^[1].

3. JIT - JAX allows you to transform your own functions into just-in-time (JIT) compiled versions using XLA^[7]. This means that you can increase computation speed by potentially orders of magnitude by adding a simple function decorator to your computational functions.

4. Auto-differentiation - The JAX documentation refers to JAX as "Autograd and XLA, brought together"^[1]. The ability to automatically differentiate is crucial in many areas of scientific computing, and JAX provides several powerful auto-differentiation tools.

5. Deep Learning - While not a Deep Learning framework itself, JAX certainly provides a more-than-sufficient foundation for Deep Learning purposes. There are many libraries built on top of JAX that seek to build out Deep Learning capabilities, including Flax, Haiku, and Elegy. We even highlighted JAX as a “framework” to watch in our recent PyTorch vs TensorFlow article, recommending its use for TPU-based Deep Learning research. JAX's highly efficient computations of Hessians are also relevant for Deep Learning, given that they make higher-order optimization techniques much more feasible.

6. General Differentiable Programming Paradigm - While it is certainly possible to use JAX in order to build and train Deep Learning models, it also provides a framework for general Differentiable Programming. This means that JAX can exploit prior knowledge in a given field, built up through decades of research, by using a model-based Machine Learning approach to solving a problem.

XLA

To jump to a summary of this section, click here.

What is XLA?

XLA, or Accelerated Linear Algebra, lies at the foundation of what makes JAX so powerful. Developed by Google, XLA is a domain-specific, graph-based, just-in-time compiler^[2] for linear algebra that can significantly increase computation speed through a variety of whole-program optimizations^[3].

In one example^[2], XLA boosts BERT training speed by almost 7.3 times from a computational standpoint alone, but lowered memory usage as a result of using XLA also enables gradient accumulation, resulting in a staggering 12 times increase to computational throughput.

XLA is baked into the very DNA of JAX - from their logos alone you can see how much the successes of JAX rely on XLA.

Why is XLA Such a Big Deal?

Answering exactly why XLA is such a big deal can yield a very technical (and long) discussion. For our purposes, it suffices to say that XLA is important because it significantly increases execution speed and lowers memory usage by fusing low-level operations.

While operation fusion (or kernel fusion) is the flagship feature of XLA, it should be noted that XLA also performs a ton of other whole-program optimizations, like specializing to known tensor shapes (allowing for more aggressive constant propagation), analyzing and scheduling memory usage to eliminate intermediate storage buffers^[4], performing memory layout operations, and only computing subsets of requested values if not all of them are being returned^[5].

Since all JAX operations are implemented in terms of operations in XLA, JAX has a unified language for computation that allows it to run seamlessly across CPU, TPU, and GPU, with library calls getting just-in-time compiled and executed^[1].

Summary

If none of the jargon above makes sense to you, don’t worry - just know that XLA is a very fast compiler which lies at the foundation of what makes JAX uniquely powerful and simple to use on a diverse range of hardware.

JAX Transformations

To jump to a summary of this section, click here.

What is a Function Transformation?

So far, we’ve talked about XLA and how it allows JAX to implement NumPy on accelerators; but recall that this was only one half of our definition of JAX. JAX provides tools not only for powerful scientific computing, but also for composable function transformations.

Quite simply, a function transformation is an operator on a function whose output is another function. If we use the gradient function transformation on a scalar-valued function f(x), then we get a vector-valued function f '(x) which gives the gradient of the function at any point in the domain of f(x).

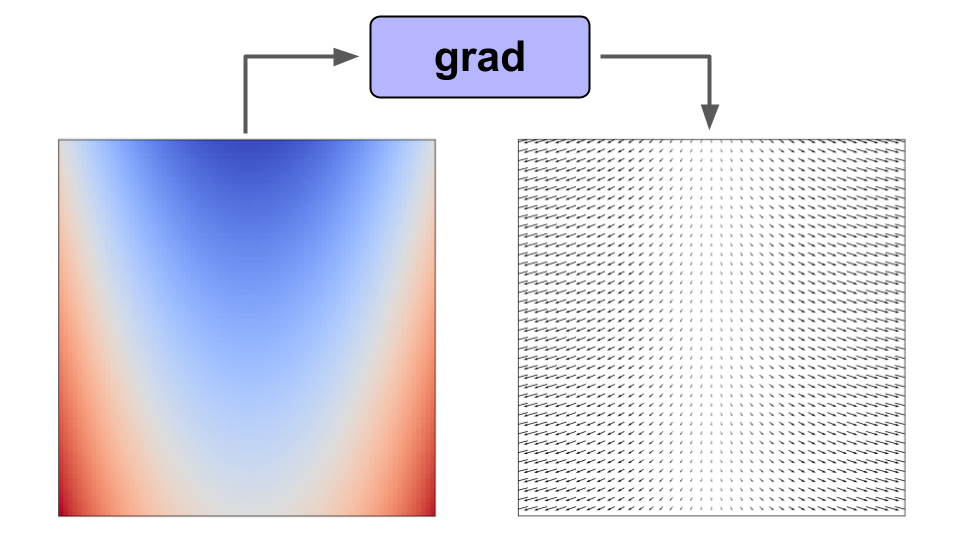
JAX incorporates an extensible system for such function transformations, and has four main transformations of interest to the typical user:

1. grad() for evaluating the gradient function of the input function
2. vmap() for automatic vectorization of operations
3. pmap() for easy parallelization of computations, and
4. jit() to transform functions into just-in-time compiled versions

Let’s take a look at each of these transformations in turn and talk about why they're so exciting. If you want to play with some interactive examples, feel free to check out our JAX Crash Course on YouTube, or it's associated Colab notebook.

Automatic Differentiation with grad()

To be able to train Machine Learning models, one needs to be able to perform backpropagation. Rather than compute the gradient of the loss function at a certain point as TensorFlow or PyTorch does by backpropagating through the computation graph, the JAX grad() function transformation outputs the gradient function, which can then be evaluated at any point in its domain.

Where Can I Differentiate?

Automatic differentiation in JAX is extremely powerful, which stems partially from JAX’s flexibility in “where” you can compute gradients. With grad(), you can differentiate through native Python and NumPy functions^[6], such as loops, branches, recursion, closures, and “PyTrees” (e.g. dictionaries).

Let’s look at an example - we’ll define a rectified cube function f(x) = abs(x3) with Python control flow. This implementation is obviously not the most computationally efficient approach, but it helps us highlight how grad() works through native Python control flow and loops nested in conditionals.

def rectified_cube(x):
  r = 1
  
  if x < 0.:
    for i in range(3):
      r *= x
    r = -r
  else:
    for i in range(3):
        r *= x
  
  return r

gradient_function = grad(rectified_cube)

print(f"x = 2   f(x) = {rectified_cube(2.)}   f'(x) =  3*x^2 = {gradient_function(2.)}")
print(f"x = -3  f(x) = {rectified_cube(-3.)}  f'(x) = -3*x^2 = {gradient_function(-3.)}")

x = 2   f(x) = 8.0   f'(x) =  3*x^2 = 12.0
x = -3  f(x) = 27.0  f'(x) = -3*x^2 = -27.0

We can see that we get the expected results when evaluating the function and its derivative at x=2 and  x=-3.

To What Degree Can I Differentiate?

JAX makes it easy to differentiate to any order by the repeated application of grad().

# for x >= 0: f(x)=x^3 => f'(x)=3*x^2 => f''(x)=3*2*x => f'''(x)=6
third_deriv = grad(grad(grad(rectified_cube)))
for i in range(5):
  print(third_deriv(float(i)))

6.0
6.0
6.0
6.0
6.0

We can see that the evaluation of several inputs to the third derivative of our function gives the constant expected output of f '''(x)=6.

From a more general perspective, the ability to take multiple derivatives in a fast and easy manner is of practical use to many more general computational fields beyond Deep Learning, such as the study of Dynamical Systems.

What Can I Differentiate?

Scalar-Valued Functions

As you would expect, grad() takes the gradient of a scalar-valued function, meaning a function which maps scalars/vectors to scalars. The gradient of such a function is useful for e.g. backpropagation, where we train a model by backpropagating from a (scalar) loss function to update our model weights.

While grad() is sufficient for a variety of projects, it is not the only type of differentiation JAX can perform.

Vector-Valued Functions

For vector-valued functions which map vectors to vectors, the analogue to the gradient is the Jacobian. With the function transformations jacfwd() and jacrev(), corresponding to forward mode differentiation and reverse mode differentiation, JAX returns a function which yields the Jacobian when evaluated at a point in the domain.

def mapping(v):
  x = v[0]
  y = v[1]
  z = v[2]
  return jnp.array([x*x, y*z])

# 3 inputs, 2 outputs
# [d/dx x^2 , d/dy x^2, d/dz x^2]
# [d/dx y*z , d/dy y*z, d/dz y*z]

# [2*x , 0, 0]
# [0 , z, y]

f = jax.jacfwd(mapping)
v = jnp.array([4., 5., 9.])
print(f(v))

[[8. 0. 0.]
 [0. 9. 5.]]

You can alternatively use a Jacobian, for example, in order to more-efficiently compute the gradient of a function with respect to a weight matrix for each datum in a data matrix.

Hessians

Perhaps one of the most exciting aspects of JAX from a Machine Learning perspective is that it makes computing Hessians exceedingly easy and efficient. Because of XLA, JAX can compute Hessians remarkably faster than PyTorch, which makes it much more practical to implement higher-order optimization techniques like AdaHessian. This fact alone could be justification enough to use JAX for some practitioners.

Let's try taking the Hessian of a simple sum of squared inputs in PyTorch:

def torch_fn(X):
  return pt.sum(pt.mul(X,X))
  
X = pt.randn((1000,))
%timeit -n 10 -r 5 pt.autograd.functional.hessian(torch_fn, X, vectorize=False)
%timeit -n 100 -r 10 pt.autograd.functional.hessian(torch_fn, X, vectorize=True)

10 loops, best of 5: 107 ms per loop
100 loops, best of 10: 3.33 ms per loop

The calculation takes about 107 ms, but using the experimental vectorizing functionality reduces execution time to 3.33 ms. Let's try the same calculation in JAX:

def jax_fn(X):
  return jnp.sum(jnp.square(X))

jit_jax_fn = jit(jacfwd(jacrev(jax_fn)))

X = jnp.array(X)
%timeit jit_jax_fn(X).block_until_ready()

The slowest run took 47.27 times longer than the fastest. This could mean that an intermediate result is being cached.
1000 loops, best of 5: 90.5 µs per loop

With JAX, the calculation takes only 90.5 µs, over 36 times faster than vectorized version in PyTorch.

Pushforwards / Pullbacks

JAX can even compute Jacobian-vector products and vector-Jacobian products. Consider a smooth map between smooth manifolds. JAX can compute the pushforward of this map, mapping tangent vectors at points on the one manifold to tangent vectors on another.

If this part is confusing or unfamiliar, don’t worry! This is an advanced topic and probably not (in and of itself) of relevance or interest to the typical user. We point out the existence of this capability simply to highlight the fact that JAX provides a very powerful foundation for a wide variety of computational tasks. For example, pushforwards are important in the field of Differential Geometry, which we might use JAX to study.

Automatic Vectorization with vmap()

Moving past the mathematical to a more practical/computational transformation, we arrive at vmap(). Consider the case in which we want to repeatedly apply a function to a set of objects. Let’s consider, for example, the task of adding two lists of numbers. The naive way to implement such an operation is to simply utilize a for loop - i.e. for each number in the first list, add it to the corresponding value in the second list, and write the result to a new list.

With the vmap() transformation, JAX performs the same computation but pushes the loop down to primitive operations for better performance^[6], resulting in an automatically vectorized version of the computation.

Of course, we could’ve simply defined our lists as JAX arrays and used JAX's array addition, but vmap() is still useful for many reasons.

One basic reason is that we can write operations in more native Python code and then vmap() it, leading to highly Pythonic and possibly more readable code. Another reason is of course generalizing to the cases in which there is no simple vectorized alternative to implement.

Automatic Parallelization with pmap()

Distributed computing has become increasingly important year-over-year, and this holds especially true in Deep Learning, where SOTA models have grown to absolutely astronomical sizes as you can see in the graph below. GPT-4, for example, will have over 100 trillion parameters.

We've discussed above how, thanks to XLA, JAX can compute on an accelerator easily, but JAX can also compute with multiple accelerators easily, performing distributed training of SPMD programs with a single command - pmap().

Consider the example of vector-matrix multiplication. Let’s say we are performing this computation by sequentially computing the dot product of the vector with each row of the matrix. We would need to push these computations through our hardware one at a time.

With JAX, we can easily distribute these computations across 4 TPUs by simply wrapping our operation in pmap(). This allows us to concurrently perform one dot product on each TPU, significantly increasing our computation speed (for large computations).

What is very noticeable here is how absolutely minimal the change to our code was. Since JAX is built on XLA, we can change how we map computations to hardware with ease.

Just-in-Time Compilation with jit()

What is Just-in-Time Compilation?

Just-in-time, or JIT compilation, is a method of executing code that lies between interpretation and ahead-of-time (AOT) compilation. The important fact is that a JIT-compiler will compile code at runtime into a fast executable, at the cost of a slower first run.

JAX's Just-in-Time Compilation

XLA primitives are JIT compiled, but JAX also lets you JIT compile your own Python functions into XLA-optimized kernels, either as a function decorator @jit or as a function itself jit()^[1].

Rather than dispatch kernels to a GPU one operations at a time, JIT will compile the sequence of operations together into one kernel using XLA, giving an end-to-end compiled, efficient XLA implementation of your function^[6][7].

To provide an example, let’s define a function which computes the sum of the first three powers of a matrix of values. We compute this function on a 5000 x 5000 matrix three times - once with NumPy, once with JAX, and once with JAX on a JIT-compiled version of the function. First, we perform the experiment on CPU:

def fn(x):
  return x + x*x + x*x*x

x_np = np.random.randn(5000, 5000).astype(dtype='float32')
x_jnp = jnp.array(x_np)

%timeit -n5 -r5 fn(x_np)
%timeit fn(x_jnp).block_until_ready()
jitted = jit(fn)
jitted(x_jnp)
%timeit jitted(x_jnp).block_until_ready()

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
5 loops, best of 5: 151 ms per loop
10 loops, best of 5: 109 ms per loop
100 loops, best of 5: 17.7 ms per loop

We see that JAX is almost 40% faster than NumPy, and when we JIT the function we find that JAX is an insane 8.5 times faster than NumPy. These results are already impressive, but let's up the ante and let JAX compute on a TPU:

In this case, we see that JAX is a staggering 9.3 times faster than NumPy, and if we both JIT the function and compute on TPU we see find that JAX is an obscene 57 times faster than NumPy.

This drastic increase in speed is, of course, not without a cost. JAX places restrictions on which functions are permissible to JIT, although functions involving only NumPy operations like the one above are generally permissible. Further, there are limitations regarding JITting through Python control flow, so you'll have to keep this in mind when writing your functions.

To learn more about JIT and its limitations, check the JAX documentation.

Summary

JAX has 4 main function transformations - grad() to automatically differentiate a function, vmap() to automatically vectorize operations, pmap() for parallel computation of SPMD programs, and jit() to transform a function into a JIT-compiled version. These transformations are (mostly) composable, very powerful, and have the potential to expedite your programs several times over.

What’s the Catch?

To jump to a summary of this section, click here.

We saw above how XLA and fundamental JAX transformations have the potential to significantly increase the performance of your programs. While JAX is very powerful and has the potential to dramatically improve productivity in a great many areas, its use requires some care. Especially if you are considering moving from PyTorch or TensorFlow to JAX, you should understand that JAX’s underlying philosophy is quite different from the two Deep Learning frameworks. We'll talk about the main difference now.

Functional Paradigm

The main characteristic that differentiates JAX is that its transformations and compilation are designed to work only for functionally pure programs. While this fact may not be relevant if you just want to use JAX to put NumPy computations on GPU or TPU, it is relevant to a huge number of potential JAX applications, so you should make sure you understand the implications of adopting this paradigm before getting started.

The central characteristic of a pure function, sometimes called numerical functions, is that of referential transparency - a pure function can be replaced with the result of its evaluation at any time, and the program cannot tell the difference. The function should always have the same effect on the program given the same inputs regardless of the time or context in which it is executed.

This sounds simple in principle, but there certainly exists a learning curve that you should be prepared for if you do not have experience in functional programming. Here are some necessary (but not sufficient!) conditions for a function to be pure:

• It cannot change the state of the program by accessing or assigning variables outside its scope
• It cannot have an I/O stream - so no printing, asking for input, or accessing the time
• It cannot have a mutable function as an argument (which a concurrent process could modify)

JAX's functional approach leads to some peculiarities which newcomers should be prepared for, like an inability to modify arrays in-place and explicit PRNG handling.

Untracked Side Effects

Side effects may not manifest themselves when running an impure function in JAX. If you are not careful, side effects like outer-scope encapsulation can silently throw off the results of your calculation. This has the potential to be catastrophic in some industries (healthcare, autonomous systems, etc.), so you should be sure that you understand how to write pure functions if you plan to utilize JAX.

Summary

JAX's function transformations are designed to work only with pure functions (sometimes called numerical functions). If you are not careful, untracked side-effects could silently throw off the accuracy of your intended computations.

Should I Be Using JAX in 2023?

As always, the answer to this question is "it depends". Whether or not advisable to migrate to JAX depends on your circumstances and goals. To help you decide if you should (or shouldn't) be using JAX in 2023, we’ve compiled our recommendations into flow charts below, with different charts for different areas of interest.

Scientific Computing

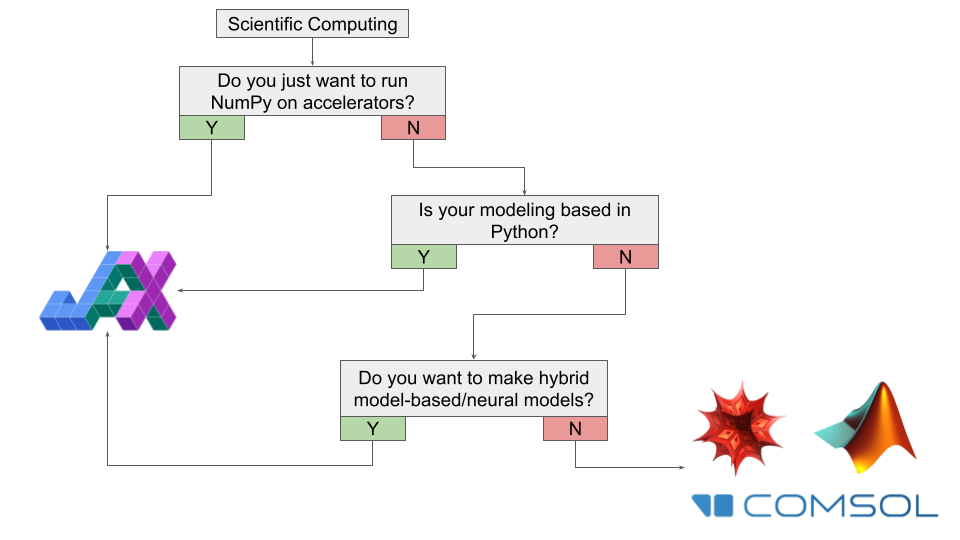
If you're interested in JAX for general scientific computing - the first question you should ask yourself is whether or not you are simply trying to run NumPy on accelerators (i.e. GPUs and TPUs). If the answer is "yes" - then you should've been using JAX yesterday. It really is a no brainer in this case, and you should start migrating to JAX.

If you are not just crunching numbers but partaking in dynamic computational modelling, then whether you should use JAX will depend on your use case. If most of your work is in Python using a lot of custom code, then it is worth it to start learning JAX in order to supercharge your workflow.

If most of your work is not in Python but you want to build some sort of hybrid model-based / neural-network system, then it is probably worth it to use JAX going forward.

If most of your work is not in Python, or you're using some specialized software for your studies (thermodynamics, semiconductors, etc.) then JAX probably isn't the tool for you, unless you want to export data from these programs for some sort of custom computational processing. If your area of interest is closer to physics/mathematics and incorporates computational methods (dynamical systems, differential geometry, statistical physics) and most of your work is in e.g. Mathematica, then it's probably worth it to stick with what you're using, especially if you have a large custom codebase.

Deep Learning

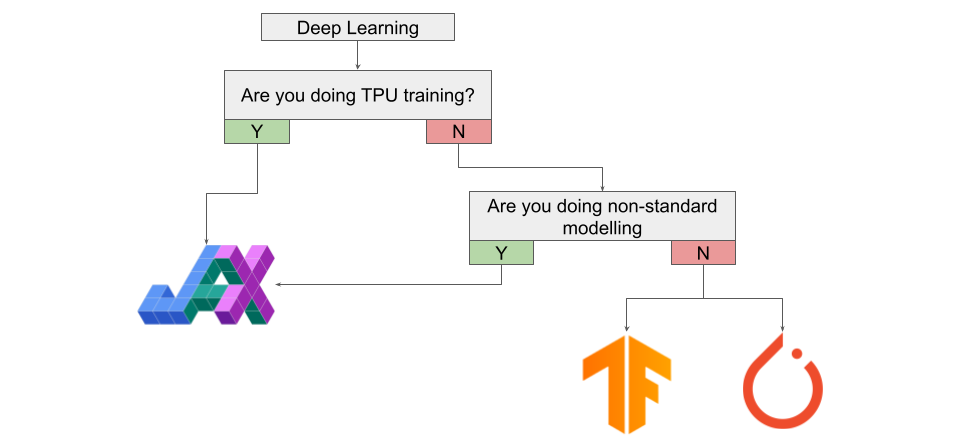
While we have emphasized that JAX is a general framework not built specifically for Deep Learning, JAX is fast and has auto-differentiation capabilities, which means that a good number of readers are surely wondering whether they should start using JAX for Deep Learning.

If you want to be training on TPUs, then you should probably start using JAX, especially if you are currently using PyTorch. While PyTorch-XLA exists, using JAX for TPU training is absolutely seamless and a much better experience overall. If you are working on "non-standard" architectures/modelling, like SDE-Nets, then you should definitely give JAX a try. Also, if you want to utilize higher-order optimization techniques, JAX should definitely be something you experiment with.

If you are not building exotic architectures and just training common architectures on GPU, then you should probably stick with PyTorch or TensorFlow for now; however, this recommendation could easily change in the coming year or two. While PyTorch still dominates the research landscape, the number of papers using JAX has steadily been growing, and with the continued development of high-level Deep Learning APIs for JAX by heavy-hitters like DeepMind and Google, in just a few short years JAX could easily see an explosive adoption rate.

In the meantime, you should still at least familiarize yourself with the basics of JAX, especially if you do any sort of machine learning research.

Beginner Deep Learning

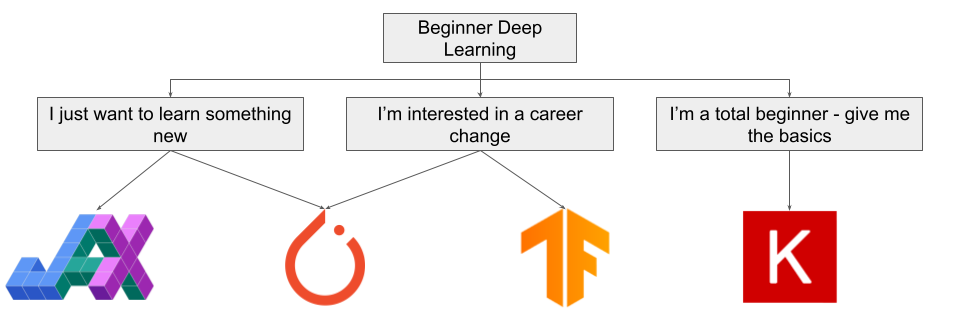
If you're just getting started with Deep Learning and are thinking about using JAX, there are a few things to consider.

If you're interested in learning about Deep Learning for your own edification, then we recommend you use either JAX or PyTorch.  If you want to learn Deep Learning from the top down and/or have some Python/software experience, then we recommend you get started with PyTorch. If you would like to learn Deep Learning from the bottom up and/or come from a mathematical background, you might find JAX intuitive and should give it a try. In this case, make sure you understand how to work with JAX before undertaking any big projects.

If you're interested in Deep Learning for a potential career change, then you'll want to use PyTorch or TensorFlow. Check out our guide here to help you choose which framework is best for you in this scenario. Although it's best to be familiar with both frameworks, you should be aware that TensorFlow is considered the "industry" framework, as evidenced by number of job postings for each framework below:

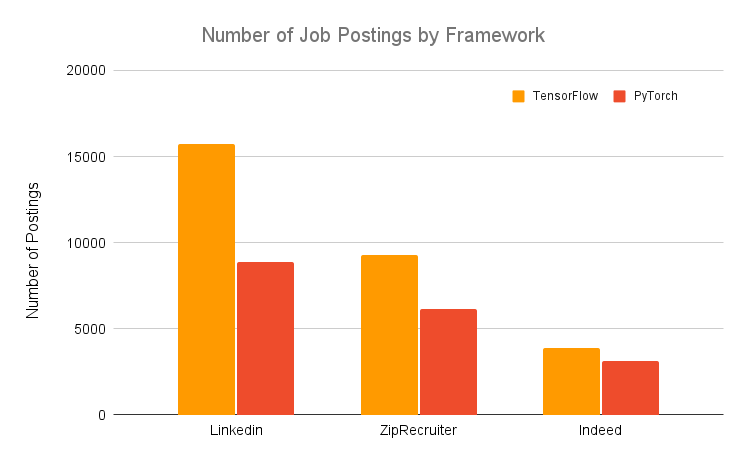
If you're a complete beginner who isn't coming from a mathematical or software background but wants to learn about Deep Learning and neural networks, then you're not going to want to use JAX. You'll instead want to start with Keras - check out our guide here for more information.

Reasons You Shouldn't Be Using JAX

While we've discussed that JAX has the potential to drastically improve the performance of your programs, here are a few reasons you shouldn't be using JAX:

1. JAX is still officially considered an experimental framework. JAX is a relatively young project - TensorFlow is almost twice as old as JAX. Currently, JAX is still considered a research-project and not a fully-fledged Google product, so keep this in mind if you are thinking about moving to JAX.

2. You have to be diligent when using JAX. The time cost of debugging or, more seriously, the risk of untracked side effects may make using JAX not worth it for those without a solid grasp of functional programming. Make sure you understand the common pitfalls of working with JAX before you start using it for serious projects.

3. JAX is not optimized for CPU computing. Per-operation dispatch is not fully optimized^[5] for JAX given that it's been developed in an "accelerator first" way. Because of this, NumPy may actually be faster than JAX in some scenarios, especially for small programs due to overhead introduced by JAX. Whether you can expect NumPy or JAX to be faster in a particular case depends on several factors - check out this page for more details.

4. JAX is not compatible with Windows. There is currently no support for JAX on Windows. If you work on a Windows machine but still want to try JAX, use Colab or install it on a Virtual Machine.

Final Words

JAX is a very promising project and has been steadily growing in popularity, despite the learning curve introduced by its functional paradigm. It will be interesting to see how JAX grows in the coming years, especially in the research community. There are already a host of projects using JAX in a variety of fields^[5]:

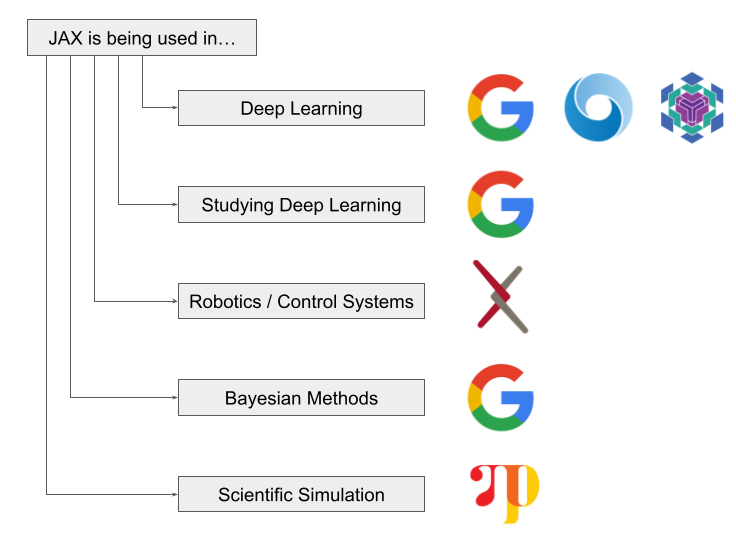
If you want to explore JAX's ecosystem, you can check out the links to some of these projects below:

We'll be dropping more JAX content in the coming months, including a deep dive into function transformations, experiments to benchmark how JAX stacks up against PyTorch and TensorFlow, and a comparison of JAX's Deep Learning APIs. Make sure to sign up for our newsletter so you don't miss it!

References

1. JAX README
2. TensorFlow 2 MLPerf Submissions
3. TensorFlow XLA
4. TensorFlow XLA Architecture
5. JAX: Accelerated ML Research via Composable Transformations
6. JAX README - Transformations
7. JAX Quickstart