Distinct fields often cross-pollinate important concepts which help drive their progress. Concepts from mathematics lay at the foundation for progress in physics; concepts from physics often inspire frameworks in economics.
Artificial Intelligence (AI) has joined this cohort, pulling in ideas from physics to develop state-of-the-art models and inform how they work at a fundamental level. While ideas from physics have been incorporated into AI before, only recently have these models outperformed other approaches in such an indomitable way with models like DALL-E 2 and Stable Diffusion.
In this article, we’ll take a high-level look at these recent advancements and show how concepts from two distinct subfields of physics - electrostatics and thermodynamics - have elevated the performance of Generative AI models to a new echelon.
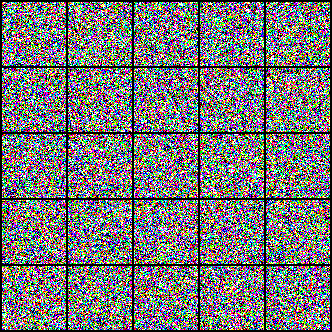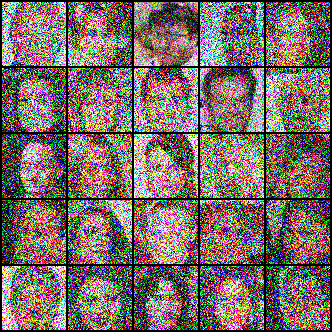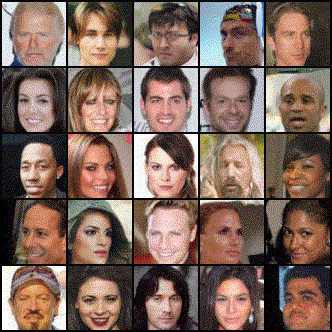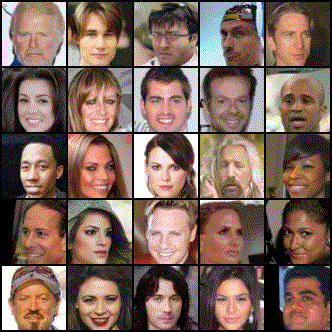
This article is geared towards anyone who is interested in the high-level concepts of how these powerful models work. We won’t get into particular mathematical details, so the explanations should be helpful to readers at all experience levels in AI.
Lessons from Electrostatics and Thermodynamics
Both of the cases we’ll look at are most often applied to Generative AI for images. For electrostatics, the treatment of a probability density as an electric charge density is the kernel of the method, where the motion of electrons according to the laws of physics can be exploited to generate novel images.
In the second case of thermodynamics, the treatment of the pixels in an image as atoms is the kernel of the method, where the natural movement of these atoms forward and backward in time can similarly be exploited to generate images.
Let’s take a look at the first case now.
Generative AI with electrostatics
Electrostatics can be viewed as the study of electric charges. Charge densities are continuous objects that have different amounts of charge in different areas. A place with a high charge density would repel (or attract) electrons with a greater force than areas with low charge density.
We can plot out the charge density of this rod - for each point on the rod we plot out “how much” charge is at that point. As we can see, there is a lot of charge in the middle, which tapers off to a lower charge at either end of the rod.
On the other hand, there are also probability densities. These curves show how likely each value of something is. Below, we show the probability density curve for the height of human males. As we can see, a male with a height of 5’11” (71 in, 180cm) is fairly likely, whereas heights much taller or shorter than this are less likely.
You may have noticed that these curves look very similar. A specific class of Generative AI model - Poisson Flow Generative Models (PFGMs) - observes this too. PFGMs work by treating a probability density as a charge density.
Specifically, to generate data we need to sample from the probability distribution of that type of data. If we want generate a sample of realistic humans (considering only height and weight), it is unlikely that they will look like this:
In particular, it is fairly unlikely to have someone that tall and thin, or that short and wide, never mind having a sample of 3 such extremes simultaneously. We need to be able to sample from the distribution according to how likely the combinations of height and weight are in order to generate more realistic novel data, like this:
With Generative AI, we attempt to use a set of example data points to learn what combinations are likely in order to generate realistic data. This set of example data points is called the training data, and it dictates what type of data we will generate. For example, if our training data are images of human faces, then we will be training the model to generate images of human faces.
How does this relate to electrostatics?
Data distribution as a charge distribution
In general, it can be hard to learn to generate samples similar to the training data. Rather than trying to do this directly, PFGMs exploit a clever trick using electrostatics to circumvent this issue.
Instead of looking at the data as a probability distribution, PFGMs change perspective and look at this distribution as a charge distribution. More likely data points (higher probability density) are considered to have more charge (higher charge density).
This, on its own, is not much help - but PFGMs utilize a crucial fact: when viewed as a charge distribution, the distribution will repel itself. Over time, this repulsion will “inflate” and gradually transform the distribution into a big uniform hemisphere. We can see a video of this process below:
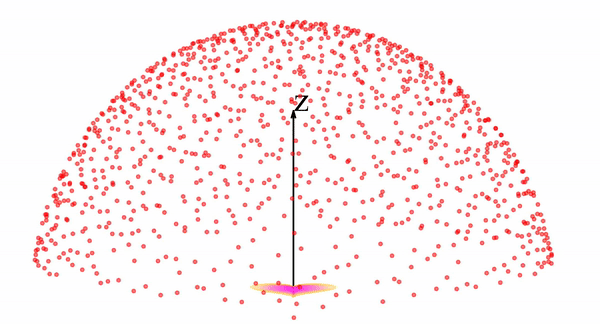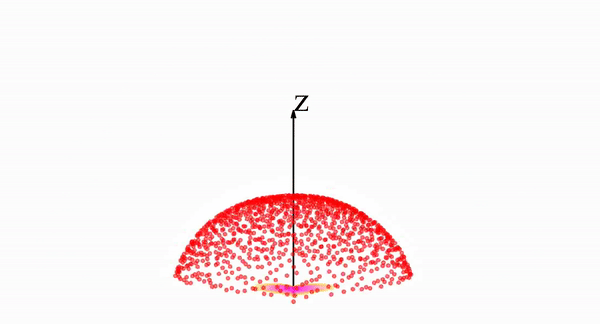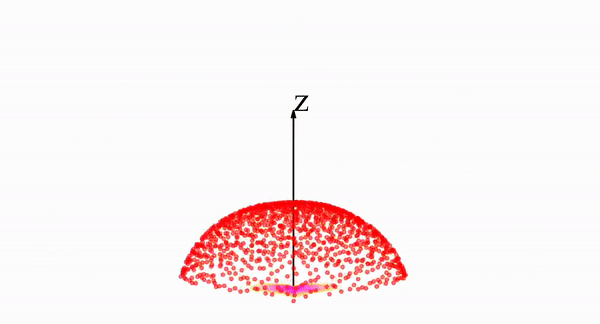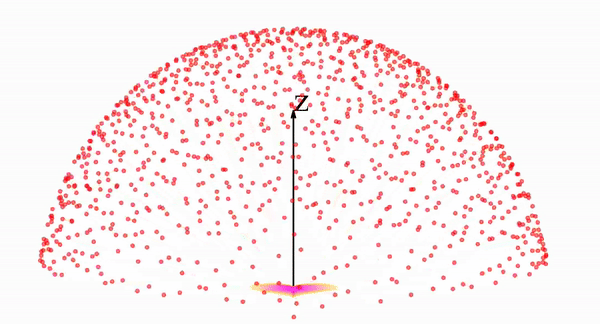
We see that the example heart shaped distribution is morphed into the hemispherical distribution by following, at each point, trajectories like those shown by the black curves below.
How does this process help us? We said earlier that it is difficult to sample from the data distribution, which is ultimately our goal. What’s not difficult is to sample from this uniform hemisphere. Since it is so uniform and regular, we can sample from the hemisphere simply by picking any point at random on it.
Let’s exploit this fact: rather than trying to model the data distribution directly and sample from it directly, we will instead sample a point on the uniform hemisphere and then use physics to map this back into the data distribution. The goal of Poisson Flow Generative Models is to learn trajectory curves like those we saw in the diagram above. These curves, which result from the laws of physics, provide the mapping between the two distributions.
Since normal forward-time physics maps the data to the hemisphere along the trajectories, we use the PFGM to go backwards in time to map in the other direction. Rather than trying to model the probability distribution of the data directly, we just model the transformation between the complicated probability distribution and the simple hemispherical distribution that we can easily choose points from.
This whole process is illustrated in the above figure. To summarize:
- Our end goal is New data. We can’t get there by directly sampling from the data distribution because it is too complicated to sample from directly.
- The Laws of physics transform this complicated data distribution into the simple hemispherical distribution
- Our PFGM learns this transformation (i.e. the trajectories) for our particular set of training data.
- We then sample from the hemisphere, which is easy to do
- Once we have this sample, we run physics in reverse-time to move backwards along these trajectories that we just learned, arriving at the data distribution and therefore generating novel data.
Don’t worry if this is confusing - it’s a tricky concept to understand. The important part is that physics provides the bridge between what we want (new data), and what we can easily get (data on the hemisphere).
We can utilize this approach too in other areas - let’s take a look at how we do that with thermodynamics for Generative AI now.
Generative AI with thermodynamics
Thermodynamics can be viewed as the study of randomness. For example, if we throw a bunch of coins on the ground randomly, we can ask how the probability of 50% of them landing heads-up compares to the probability of 100% of them landing heads up.
Let’s look at the case of four coins. The probability that 100% (four) of them land heads-up is less than the probability of just 50% (two) of them landing heads-up. This is because there are six ways for only two coins to land heads-up, while there is only one way for all four coins to land heads-up.
In this case, we see that 50% of the coins being heads-up is 6 times more likely than 100%. If we extend this same thought-experiment to ten coins, then 50% (five) of the coins landing heads-up is 252 times more likely than 100% (ten) of them landing heads-up. If we extend this to just fifty coins, then this factor becomes 126 trillion times more likely. What if we extend this concept to billions of coins?
From coins to atoms: Diffusion
Thermodynamics casts atoms as “coins” and studies the consequences of the above phenomenon in physical systems. For example, if a drop of food coloring is placed into a glass of water, the food coloring spreads out to eventually create a uniform color in the glass. Why is this?
The uniform color is a result of the atoms of food coloring spreading out over time. There are many more ways for the billions of atoms to be in different places than all in the same place, just as there are many more ways for 50% of coins to land heads-up than 100% of them. When all of the atoms are concentrated in a single drop, they can be considered to be “100% heads-up”; when the atoms are spread out evenly, they can be considered to be “50% heads-up”.
Remember, the “50% heads-up” state is more likely, and only becomes more likely as the number of coins grows - it was 126 trillion times more likely with only 50 coins. When we consider atoms as coins, we must keep in mind that there are trillions of billions of atoms in just a drop of food coloring. With this number of atoms, it becomes overwhelmingly more likely that they will end up spread out than in a concentrated drop. So, simply through random motion, the drop will spread out over time as it approaches this 50% state of uniform color.
This process is called diffusion, and it inspires models like DALL-E 2 and Stable Diffusion.
From atoms to pixels: Diffusion in Generative AI
Just as thermodynamics views atoms as coins, Diffusion Models view the pixels of images as atoms. Similarly to how the random motion of food coloring will always lead to a uniform color, the “random motion” of pixels will always lead to “TV static”, which is the image equivalent of uniform food coloring.
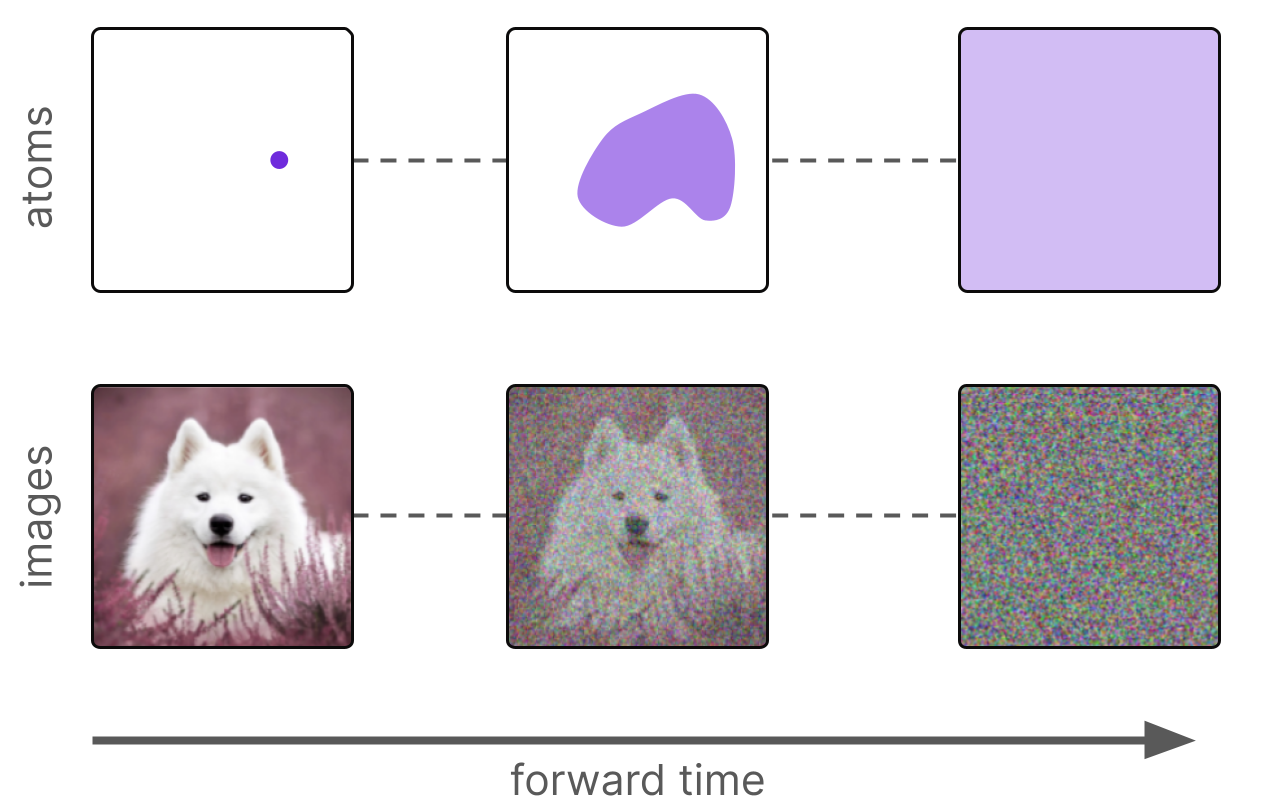
Importantly, no matter where we place the initial drop of food coloring, over time all possible starting positions will yield this same final state of uniform color.
Note in particular that it is impossible to go backward and figure out where the drop initially was from this uniform state since all initial states lead to it. The lack of injectivity makes it impossible to go backward in general.
We always know how drops will diffuse in forward time, but we don’t know how to reverse-diffuse the uniform coloring due to this issue of injectivity. However, if we relegate our concerns to one particular drop, then we can model this process both forward and backward in time.
Diffusion Models use this same principle in the image domain. In particular, the different “drops” for Diffusion Models correspond to different types of images. For example, these drops could correspond to images of dogs, images of humans, and images of handwritten digits.
By picking just one type of image, say images of dogs, Diffusion Models can learn to go backwards in time for that one type of image, just like how we can learn to go backwards in time from the uniform color by picking just one drop.
Image generation with Diffusion Models
It may be unclear why we would want to do this - if we have a dataset of images of dogs, why would we want to go forward and backward like this? The answer lies in the fact that the figure directly above is slightly deceptive - a particular image of a dog is not analogous to the drop of food coloring - it is the entire class of images of dogs that is analogous to the drop of food coloring.
Particular images of dogs are actually analogous to particular atoms in the drop of food coloring. Recall from above that relegating our concerns to one initial drop allowed us to model the diffusion process forward and backward in time.
Understanding how the diffusion process works in reverse-time allows us to trace individual atoms back to their starting points in the drop. In particular, we pick a random atom from the uniform food coloring, and then reverse time to see where in the initial drop of food coloring it started from.
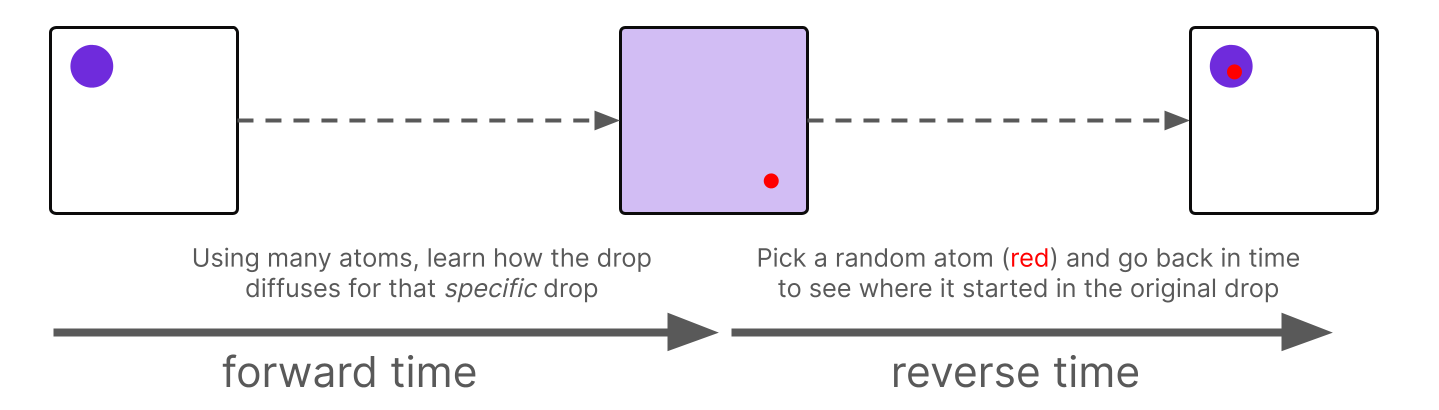
We mimic this process with Diffusion Models. Analogously, we pick a random image of TV static (“atom”) and then go backwards through time to figure out where it started in the data distribution (“initial drop”). That is, we determine which image of a dog led to that image of TV static in forward-time.
This process is very similar to PFGMs. With PFGMs, we modeled the physics that maps our data distribution to a uniform hemisphere. Since the hemisphere is easy to sample from, we pick a point on it and run physics in reverse-time to generate a new image. With Diffusion Models, we model the physics that maps our data distribution to TV static. Since TV static is easy to generate, we pick a random image of TV static and run physics in reverse-time to generate a new image.
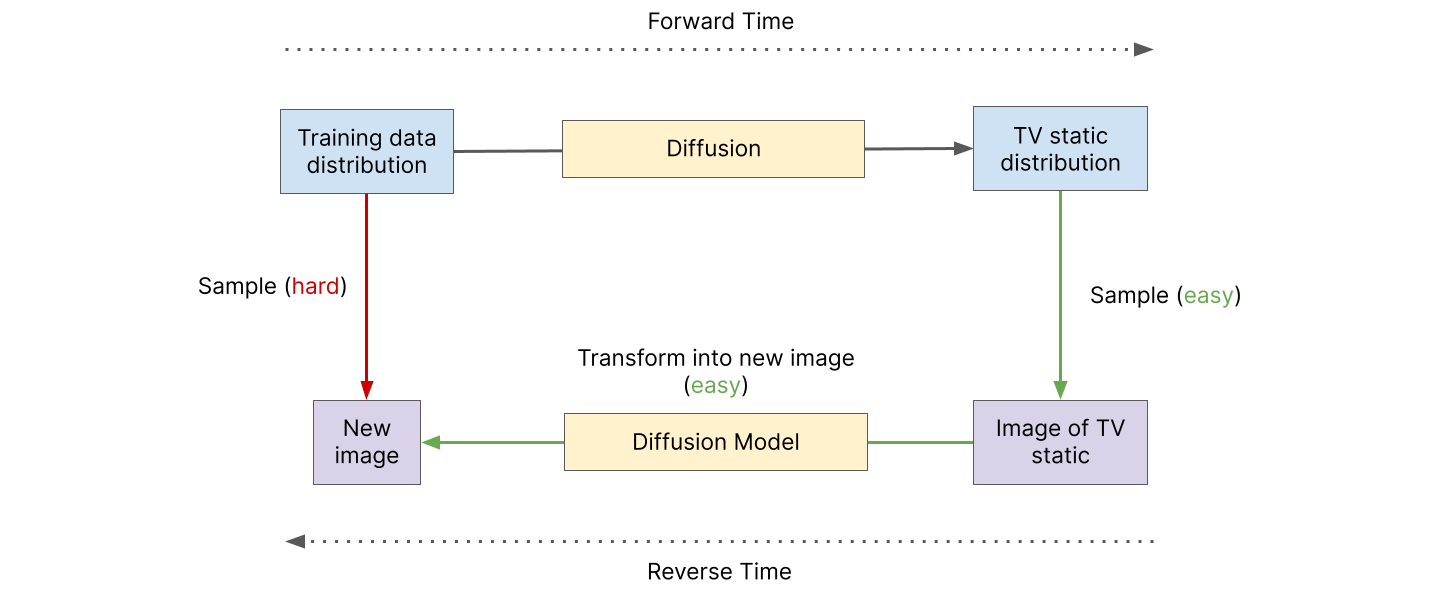
Diffusion Models lie at the foundation of much of the progress in Generative AI in the image domain. Text-to-image models like Imagen and DALL-E 2 augment this process, allowing us to tell the model what we want the generated image to look like.
Final Words
Many of the recent advancements in Artificial Intelligence are inspired by ideas from physics. As we have seen, these high-level ideas lie at the foundation of modern methods in Generative AI, powering the newest generation of AI models.
If you enjoyed this article, feel free to check out some of our other articles to learn about the Emergent Abilities of Large Language Models or How ChatGPT actually works. Alternatively, feel free to subscribe to our newsletter to stay in the loop when we release new content like this.